Bestimme alle Punkte oder Funktionen, die folgende Gleichung erfüllen:
Ansatz a+ib (oder x+iy)
Ggf. Quadratische Ergänzung
Ggf. Definitionsbereiche und Wertebereichseinschränkungen
|
1 |
|
Aufgabenstellung (Definitionsbereiche und Wertebereiche) |
|
2 |
|
Einsetzen des Ansatzes |
|
|
|
Umformungszwischenschritte der rechten und linken Seite der Gleichung. |
|
3 |
|
Ein wichtiges Zwischenergebnis. (Definitionsbereiche und Wertebereiche) |
|
|
|
Quadrierung (ggf. kommen hierbei weitere Lösungen hinzu.) |
|
|
|
|
|
|
|
|
|
4 |
|
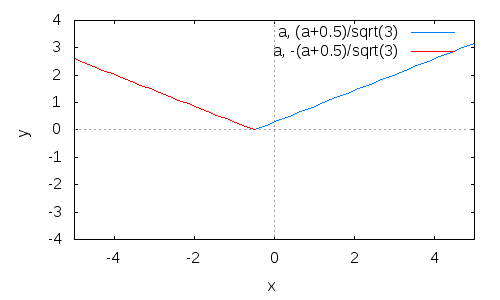
In dem Falle ergeben sich als Lösung zwei Geradengleichungen.
|
In dem Falle ergeben sich als Lösung zwei Geradengleichungen. Diese sind auf Ihre Gültigkeit zu überprüfen.
Wegen folgender Gleichung dürfen die y-Werte nur positiv sein:
Also sind die Fallunterscheidungen für die verschiedenen Äste noch zu treffen und zu prüfen, ob diese auch Lösung der Gleichung sind.
für
für
Für streben (oder sind) beide Lösungen nach . Somit sind die Funktionen stetig. Wegen der unterschiedlichen Steigungen sind diese an dem Punkt nicht differenzierbar.
wxplot2d([[parametric,a,1/sqrt(3)*(a+0.5),[a,-0.5,5]],[parametric,a,-1/sqrt(3)*(a+0.5),[a,-5,-0.5]]], [x,-5,5], [y,-4,4], [nticks,20])$
